Lasso & Ridge Regression
Ridge 和 Lasso 就是基於回歸的方法做出的改良,回歸的解釋性很強,但其容易有在多變數的情況有過擬合的情況。從回歸的目標函是來找出 Lass 和 Ridge 的改良過程。
從殘差平方和 $RSS$ 到 $R^2$
RSS
線性回歸是使用殘差平方和 $RSS$(residual sum of squares)透過最小二乘估計來算出最佳的的截距和斜率。
$$ RSS = \sum_{i=1}^n (y_i - \hat{y})^2 = \epsilon_1^2 + \epsilon_2^2 + \dotsb + \epsilon_n^2 $$
$MSE$ & $RSE$
因為 RSS 會隨著樣本數增加而增加,估將其平均為均方誤差 MSE(mean squared error),而將 MSE 開方後就式 RSE(Residual Standard Error)
$$ MSE = \frac{1}{n}\sum_{i=1}^n(y_i - \hat{f}(x_i))^2 = \frac{1}{n}RSS = RSE^2 $$
$TSS$
但是 RSE 的單位是以 $y$ 來計算,故沒有統一的衡量標準,故在測量的標準無法統一,故導入 TSS(Total Sum of Square)
$$ TSS = \frac{1}{n}\sum_{i=1}^n(y_i - \bar{y} )^2 $$
$R^2$
從公式就可以看出 $TSS$ 其實就是 variance 的和,表示原有資料中應變量的變異程度。而 $RSS$ 表示的是模型無法解釋的誤差,那麼 $TSS−RSS$ 就是模型可以解釋的誤差,再除以 $TSS$ 就是模型可以解釋的誤差佔比,因此 $R^2$ 表示的是模型擬合更好的情況, $R^2$ 是比例的概念,因此範圍在 0 與 1 之間。
$$ R^2 = \frac{TSS- RSS}{TSS} $$
多變數線性迴歸
回到回歸,一般來說特徵值不會只有一個,因此會有多變數線性回歸的問題,以下為多變數線性回歸方程式表示如以下。
$$ \hat{y} = w[0] \times x[0] + w[1] \times x[1] + \dotsb w[n] \times x[n] + b $$
b 和 w 為模型最終學到的參數(parameter)和係數(coefficient),x 則為特徵值,n 則為特徵數量。w 也可以說是影響特徵值的權重。
線性回歸因為透過 RSS 尋找最佳的參數(parameter)和係數(coefficient),而但當特徵值過多時,以及有共線性的特徵值產生 coefficient 的值很容易過大,導致整個模型過擬合。因此我們要降低其權重。
懲罰值
如上述特徵是用 coefficient 來估計其對於方程式的變化或權重,因此若能限制或歸 0 部分的特徵值係數,則能減少模型的光滑度(flexibility)來避免高 variance。因此透過正規化 regulariztion 降低模型的複雜度,Lasso 和 Ridge 都是基於線性回歸模型防止過擬合的工具,只要應用 Lasso 或者 Ridge,都需要對特徵進行標準化(standardized)。
而正規化就是在原有的 RSS 中加入懲罰值 P
$$ mininize ={RSS + P} $$
Ridge
Ridge 迴歸的懲罰值則是加入了 $ \lambda $ 來最小化 coefficient,而這個方式稱為 L2 norm,當 $ \lambda $ → 0 時,則和一般迴歸一樣。目標函式則為原有的 RSS,$ \lambda $ 越大則懲罰效果越大,迫使所有 coefficient 趨近於 0
相較於 Ridge 的優點
- 當有多元共線性時,會將高度相關的特徵保留,而非像 Lasso 會隨機選擇其一併將其他特徵歸 0
$$ RSS + \lambda \sum_{J=1}^p\beta_j^2 $$
以下 snippet 顯示 $ \lambda $ 的變化對於 coefficient 收斂的效果,這邊我先載入 sklearn 的 Boston 房價資料,其為 tuple 的資料型態,剛好分為將其分為 X, y,然後 split 成 training set 和 test set
import mglearn.datasets
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt
from mglearn.datasets import load_extended_boston
from sklearn.linear_model import Ridge
boston = load_extended_boston()
X, y = boston
X_train, X_test, y_train, y_test = train_test_split(
X, y, random_state = 123)
然後用 np.logspace,產生等比數列來看 $ \lambda $ 變化對於 coefficient 係數的影響
ridge = Ridge().fit(X_train, y_train)
clf = Ridge()
coefs = []
alphas = np.logspace(-7, 7, 200)
for a in alphas:
clf.set_params(alpha = a)
clf.fit(X_train, y_train)
coefs.append(clf.coef_)
plt.style.use('fivethirtyeight')
plt.figure(figsize = (40, 20))
plt.subplot(121)
ax = plt.gca()
ax.plot(alphas, coefs, color = 'peru')
ax.set_xscale('log')
plt.xlabel('alpha')
plt.ylabel('weights')
plt.title('Ridge coefficients as a function of the regularization Alpha parameter')
plt.axis('tight')
plt.grid(color = 'black', linestyle = 'dotted')
plt.show()
可以看的出來 coefficient 在 $10^{-4}$ 左右時開始快速收斂,當接近 $10^{-1}$ 實則 coefficient 幾乎趨近於 0,但 Ridge 沒有 feature selection 的功能,故 coefficient 不會收斂為 0
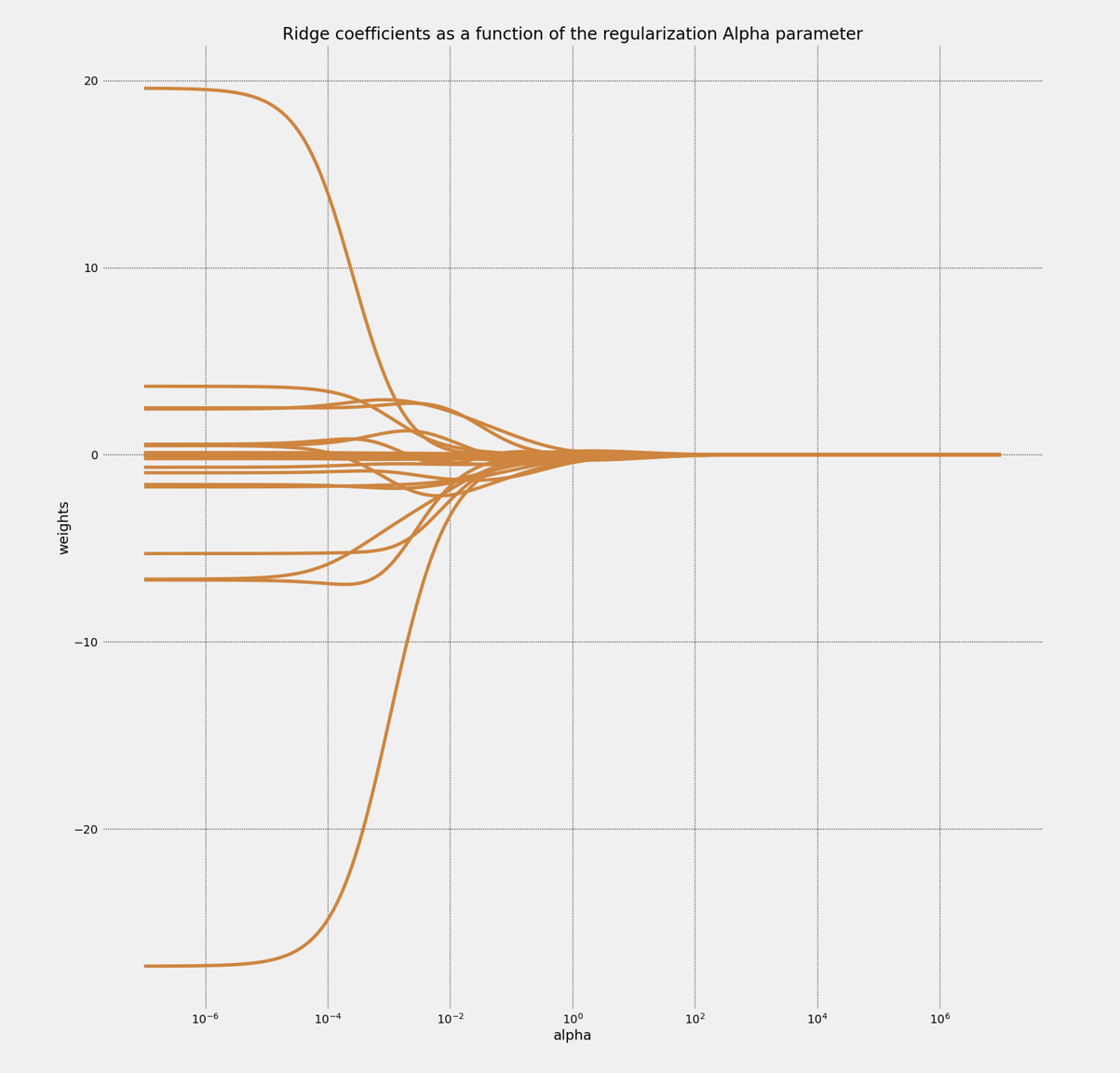
我們可以針對 Ridge 訓練集和測試集看一下 $R^2$
ridge = Ridge(alpha = 0.1).fit(X_train, y_train)
print("Test set socre: {:.2f}".format(ridge.score(X_test, y_test)))
print("Training set socre: {:.2f}".format(ridge.score(X_train, y_train)))
Test set socre: 0.77 Training set socre: 0.93
可以對比一下單純的 Linear Regression,其 training set 的擬合程度非常高,但 test set 的 score 就低於正規化後的 Ridge model
lr = LinearRegression.fit(X_train, y_train)
print("Test set socre: {:.2f}".format(ridge.score(X_test, y_test)))
print("Training set socre: {:.2f}".format(ridge.score(X_train, y_train)))
Test set socre: 0.61 Training set socre: 0.95
Lasso
Lasso 正規化的方式稱為 L1 norm,其可以有 feature select 的效果,可以將特徵值的 coefficient 係數收斂為 0
相較於 Ridge 的優點
- 可以做自動做特徵選擇。因此可以用在超多特徵的數據中,提供了稀疏的解決方案
Lasso 的目標函式如以下 $$ RSS + \lambda \sum_{J=1}^p| \beta_j | $$
from sklearn.linear_model import Lasso
lasso = Lasso(alpha = 0.01, max_iter = 100000).fit(X_train, y_train)
print("Test set socre: {:.2f}".format(lasso.score(X_test, y_test)))
print("Training set socre: {:.2f}".format(lasso.score(X_train, y_train)))
Test set socre: 0.77 Training set socre: 0.90
referance
https://www.zhihu.com/question/38121173
https://www.cnblogs.com/wuliytTaotao/p/10837533.html
Explaining the Bias-Variance Trade-off in Machine Learning