生存分析(survival analysis)
生存分析,生存分析最初是由精算師和醫學界大量開發和應用的,他主要是針對特定事件發生地當下,以及探討在事件發生以前所持續時間的長短 (生存時間) 的一種分析方法。
生存分析可以說是一種 Time to Event 的框架
套用到行銷或商業上就能有以下類似命題:
- 用戶流失這個事件的判斷,以及用戶流失前持續的活躍時間
- 信用卡剪卡的事件判斷,以及用戶持續使用信用卡的時間
那就有幾個很重要的問題:
- 事件的起始判斷點
- 如何判斷事件發生的明確定義
第一點,也就是要確定用戶何時開始算入整個分析的環節,例如是以註冊完後就開始計算,還是參加了某個活動。以信用卡的例子也可以想程式辦卡開始算還是第一次刷卡
第二點,如何判斷特定事件已經發生,就醫學上的例子,如果人失蹤了,那就算死亡嗎,假設以生存分析來看,受測者在實驗過程中失蹤了,那怎麼去定義是否事件發生
因此這類型其事件發生與否會跟著時間變量反映的,無法透過一般的模型去預測,會很容易低估,因為模型訓練當下未發生事件的。
生存分析基本概念匯總:
- 事件(event):例如死亡、疾病發生、合約終止等; 本文中提到的事件是指用戶活躍,例如使用者是否打開APP。
- 存留時間(t):從觀察期開始到事件發生的時間。 例如手術或開始治療的時間、上次到下次打開APP的時間等。
- 刪失(censorship):在觀察期間內(last follow-up)沒有觀測到事件發生。
因此在留存分析中如果定義客戶解約為結束事件,那在沒有實際解約前,但卻不活躍的客戶就可以視為 censorship
- 風險中的數量:在觀察期內可追蹤其狀態且未發生事件的對象數量。
而 censorship 的數據,一般也還是會列入數據統計中,雖然其在離開實驗前未發生事件,但仍其存留時間仍是可以列入模型考量。
以信用卡為例,假如我的事件判定是客戶剪卡不使用該卡為事件發生。但在客戶未剪卡之前被盜刷而被停卡,或是繳不出卡費被停卡這都可以被視為 censorship。
導入數據
先導入 data,這邊先使用 Kaggle 的 data 做說明,數據連結如下
看一下 data 的狀態
df = pd.read_csv("../data/WA_Fn-UseC_-Telco-Customer-Churn.csv")
train_df, test_df = train_test_split(df, random_state = 123)
train_df.head()
| customerID | gender | SeniorCitizen | Partner | Dependents | tenure | PhoneService | MultipleLines | InternetService | OnlineSecurity | OnlineBackup | DeviceProtection | TechSupport | StreamingTV | StreamingMovies | Contract | PaperlessBilling | PaymentMethod | MonthlyCharges | TotalCharges | Churn | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6464 | 4726-DLWQN | Male | 1 | No | No | 50 | Yes | Yes | DSL | Yes | Yes | No | No | Yes | No | Month-to-month | Yes | Bank transfer (automatic) | 70.35 | 3454.6 | No |
| 5707 | 4537-DKTAL | Female | 0 | No | No | 2 | Yes | No | DSL | No | No | No | No | No | No | Month-to-month | No | Electronic check | 45.55 | 84.4 | No |
| 3442 | 0468-YRPXN | Male | 0 | No | No | 29 | Yes | No | Fiber optic | No | No | Yes | Yes | Yes | Yes | Month-to-month | Yes | Credit card (automatic) | 98.80 | 2807.1 | No |
| 3932 | 1304-NECVQ | Female | 1 | No | No | 2 | Yes | Yes | Fiber optic | No | No | Yes | No | No | No | Month-to-month | Yes | Electronic check | 78.55 | 149.55 | Yes |
| 6124 | 7153-CHRBV | Female | 0 | Yes | Yes | 57 | Yes | No | DSL | Yes | No | Yes | Yes | No | No | One year | Yes | Mailed check | 59.30 | 3274.35 | No |
先理解一下 data 的欄位:
Churn:一般泛指用戶退租、不繼續使用或不再繼續在這個平台活躍,是生存分析中的事件發生與否
tenure:目前持續的存留時間,包含未發生事件或是已發生事件而確定的存留時間
為何不使用一般模型 ?
這邊我們希望預測的是要了解我們對某事發生之前的時間感興趣,或者某事是否會在某個時間範圍內發生。
一般的回歸模型或是分類模型處理的是截面數據,只關注事件的結果(例如是否有購買); 但生存分析不僅關注事件的結果,還將事件發生的時間納入了模型的分析框架,能夠有效刻畫事件的發生時間,以及事件隨時間變化的規律。
train_df[["tenure", "Churn"]].head()
| tenure | Churn | |
|---|---|---|
| 6464 | 50 | No |
| 5707 | 2 | No |
| 3442 | 29 | No |
| 3932 | 2 | Yes |
| 6124 | 57 | No |
1. Churn = ‘Yes’
如果要根據一般的模型來預測,第一種那就需要先考慮 Churn = 'Yes'
train_df_churn = train_df[train_df['Churn'] == 'Yes']
如果以這樣的 table 做 prediction 留存時間會遇到甚麼問題?
留存時間會被 under estimator
平均而言,預測會被低估,因為我們忽略了當前訂閱(未流失)的客戶。我們的數據集是在數據收集的時間視窗內流失的人的有偏見的樣本。
2. 假設每個人都正在流失
使用原始 table,但這又會遇到甚麼問題?
留存時間仍舊會被低估。
這是因為仍然留存的人未被刪除,因此其留存時間應該預計會更長,因此我們在這個時間點作的紀錄,往往會比總體的留存時間還要短。
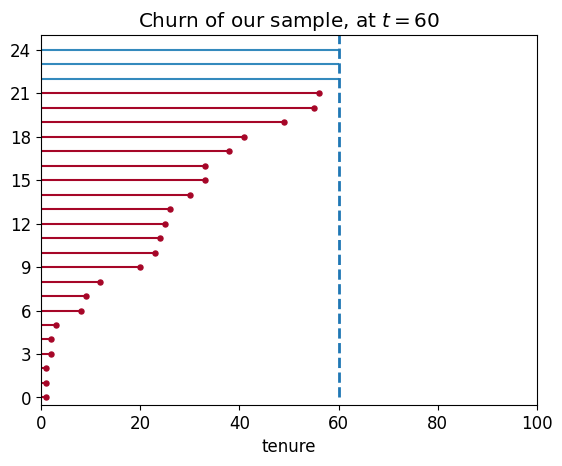
這邊使用視覺化來呈現這種預測的狀態,隨機抽取 25 個觀測對象,並假設當下做分析時 tenure = 60。
from lifelines.plotting import plot_lifetimes
import numpy as np
from numpy.random import uniform, exponential
CURRENT_TIME = 60
sampled_train_df = train_df.sample(n = 25, replace = False)
actual_lifetimes = np.array(sampled_train_df ['tenure'])
observed_lifetimes = np.minimum(actual_lifetimes, CURRENT_TIME)
death_observed = actual_lifetimes < CURRENT_TIME
ax = plot_lifetimes(observed_lifetimes, event_observed = death_observed)
ax.set_xlim(0, 100)
ax.vlines(60, 0, 30, lw = 2, linestyles = '--')
ax.set_xlabel("tenure")
ax.set_title("Churn of our sample, at $t=60$")
可以看到藍色的兩條線,其實際 tenure 的值是大於 60,但因為我們檢測生存長度的當下 $t$ = 60,因此我們只能觀測到最大的 t = 為 60,因此在最預測時就往往會低估了實際的生存時間。
生存分析基本概述
開始生存分析中首先要釐清資料的相關定義
- 對於結果/事件的定義
- 研究的時間起點
- 研究的時間單位是用的月份,周,還是年,是觀察時間,還是患者的實際年齡 (實際年齡就是實際生存時間)
- 事件發生時的時間,是否被精確定義了?
而生存分析中重要的函數如下
生存方程(函數)
觀測生存時間 $T$,大於某個時間 $t$ 的機率: $$ S(t) = Pr(T \geq t) $$ 其反映的是研究對象到該時刻仍未發生事件的機率
風險函數
$$ h(t) = \frac{f(t)}{S(t)} $$
風險函數可以想成到時刻 $t$ 時存活下來的個體在此後一個無限小的時間區間內事件(失效、死亡)發生的概率
醫學統計學·第四版書中也稱為
已生存到時間 t 的觀察物件在 t 時刻的暫態死亡率。
累積風險函數
也就是指生存時間不超過某個時間點 $t$ 的機率 $$ H(t) = \int\limits_t^0 h(u)du $$
中間推導過程就略過 🕺🏻,最後險是生存函數 $S(t)$ 和風險函數 $h(t)$ 的關係 $$ S(t) = \exp{ -\int\limits_t^0 h(u)du} = \exp{-h(t)} $$
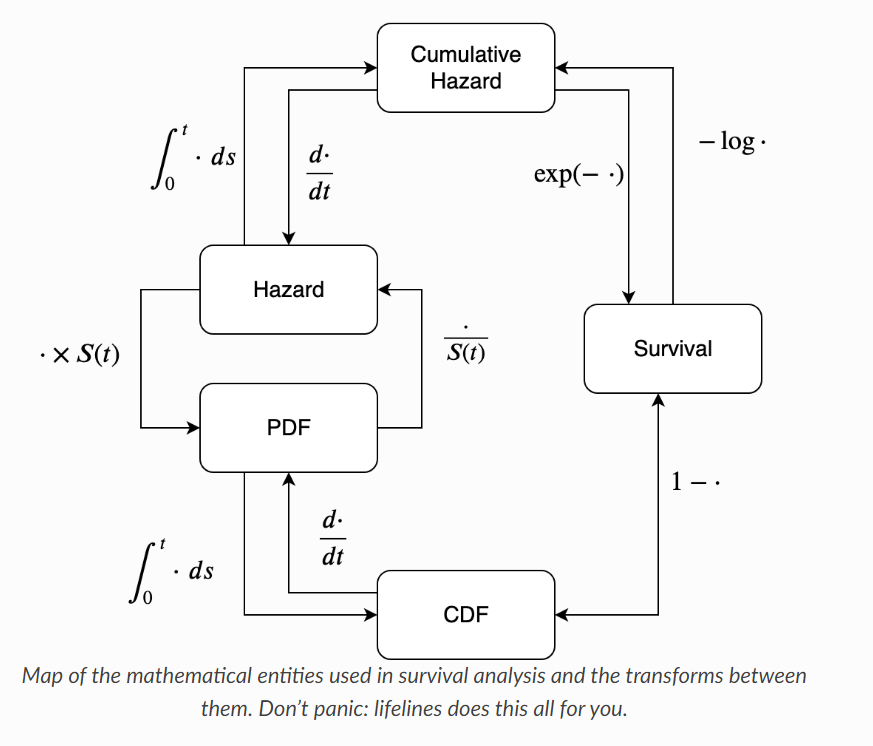
總結一下,一般來說會針對 censorship 刪失的資料做生存函數的估計,而對於發生了實際事件的資料使用機率密度函數來估計該數據的最大似然估計
那既然用傳統的模型去估計留存時間會低估,那就要進入生存分析啦
一般來說生存分析的方法總共分成兩類。
- 參數估計:參數法假定存留時間符合某種分佈(如指數分佈、威布爾分佈、對數正態分佈等),根據樣本觀測值來估計假定分佈模型中的參數,以獲得存留時間的概率密度模型。
- 非參數估計
生存分析中的非參數法
- 非參數法可以對生存時間不必進行任何參數分布 (parametric assumption) 的假設,初步地估計生存方程和累積風險度方程;
- 使用非參數法可以用生存曲線圖的方式直觀地展示生存數據,包括刪失值在數據中的存在也可以通過圖表來表現出來;
- 非參數法可以初步地對不同組之間生存曲線的變化進行比較;
- 通過非參數法對生存數據進行初步分析之後,可以對其後更加複雜的生存數據建模過程提供有參考價值的背景信息。